Résumé
Dans un texte précédent, j’ai explicité l’interprétation probabiliste des « marges d’erreur » dans les sondages. J’ai aussi montré comment il est possible d’aller au-delà en considérant des énoncés complexes. Cette note considère la question de la « probabilité pour un candidat d’être au second tour », sur la base des récents sondages relatifs au premier tour de l’élection présidentielle de 2017.
1 Les écarts se resserrent
Les derniers sondages relatifs au premier tour de l’élection présidentielle du 23 avril 2017 indiquent un resserrement des écarts entre 4 candidats : Macron, Le Pen, Fillon et Mélenchon, chacun se trouvant crédité de 18.5% à 24.5% d’intentions de vote selon les cas. Et les commentateurs de souligner que « on est dans la marge d’erreur » et que les résultats du vote deviennent de ce fait de plus en plus difficiles à anticiper.
Je me propose de contribuer à ce débat en calculant, pour chacun de ces candidats, la probabilité d’être présent au second tour de l’élection au vu des sondages récents.
Cette note fournit ces résultats pour 4 sondages, sur la base des données disponibles à partir de la synthèse fournie par Wikipedia (2017) :
• sondage BVA, POP 2017, d’avril 2017 (vague 17), réalisé les 12–14 avril 2017, sur un échantillon de 1439 personnes inscrites sur les listes électorales (dont n=1044 exprimant une intention de vote) ;
• sondage IFOP-Fiducial (sondage de type « rolling ») pour Paris-Match, CNews & Sud Radio, réalisé les 11–14 avril 2017, sur un échantillon de 2776 personnes inscrites sur les listes électorales (dont n=1915 exprimant une intention de vote, effectif total obtenu indirectement) ;
• sondage Odoxa pour Le Point, réalisé les 12–13 avril 2017, sur un échantillon de 950 personnes inscrites sur les listes électorales (dont n=754 exprimant une intention de vote) ;
• sondage IPSOS pour Le Monde, réalisé les 12–13 avril 2017, sur un échantillon de 1509 personnes inscrites sur les listes électorales (dont n=927 exprimant une intention de vote) ;
Le tableau suivant donne, pour chacun de ces sondages, les fréquences et les effectifs des candidats Macron, Le Pen, Fillon, Mélenchon & Hamon :
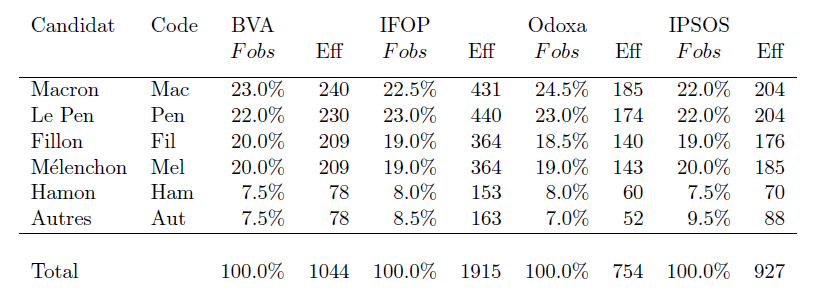
[Remarque : Les effectifs ci-avant ont été reconstitués à partir de l’effectif total et des fréquences fournies, qui sont arrondies à 0.5% près, d’où de possibles légers écarts par rapport aux données réelles, qui elles ne sont pas disponibles.]
2 Rappel : Interprétation probabiliste des marges d’erreur
Dans un texte précédent sur ce blog (Bernard, 2017a), j’ai explicité comment la marge d’erreur associée à une fréquence (proportion) pouvait s’interpréter de façon probabiliste. Par exemple, pour le candidat Macron et le sondage BVA, la fréquence observée est Fobs=23.0%, obtenue sur n=1044 répondants, d’où une marge d’erreur de MErr=2.6% (à la garantie 0.95=95%). En terme de probabilité, ceci peut s’exprimer par un énoncé portant sur la fréquence réelle, Freel, sousjacente :
Prob(Fobs − MErr < Freel < Fobs + MErr) = 0.95, Prob(23% − 2.6% = 20.4% < Freel < 23% + 2.6% = 25.6%) = 0.95 (1)
Au vu des données, n et Fobs, on peut dire, avec une garantie (ou niveau de confiance) 95% que la fréquence réelle Freel d’intentions de vote pour Macron est comprise entre 20.4% et 25.6%.
3 Probabilité d’un candidat d’être au second tour
Dans Bernard (2017a), j’ai montré comment il est possible d’aller au-delà, en calculant la probabilité de n’importe quel énoncé d’intérêt sur une ou plusieurs fréquences réelles. Dans le sondage BVA, ce sont Macron et Le Pen qui arrivent en tête et qui seraient donc qualifiés pour le second tour. Mais cette propriété observée sur les données, i.e. sur les Fobs, est-elle assurée d’être également vraie sur les fréquences réelles, les Freel, qu’on obtiendrait si on avait pu interroger non pas n=1044 individus, mais la population entière des votants ?
Les mêmes méthodes d’inférence bayésienne que celles évoquées dans Bernard (2017a), et mises en oeuvre dans le logiciel BayCat-5 (Bernard, 2017b), permettent de répondre à ce genre de question. Plus précisément, nous avons calculé, la probabilité que chaque candidat soit en fait parmi les deux premiers, i.e. que sa fréquence réelle soit la première ou la seconde parmi toutes les fréquences réelles. Si on note Rang(Freel) le rang (pouvant aller de 1 à 11) de chacune des fréquences réelles des 11 candidats qualifiés, j’ai donc calculé :
Prob( Rang(Freel[Mac] = 1 ou 2) ) (2)
pour Macron, et ce de même pour chaque candidat. Ce calcul a été réalisé pour chacun des 4 sondages pris isolément.
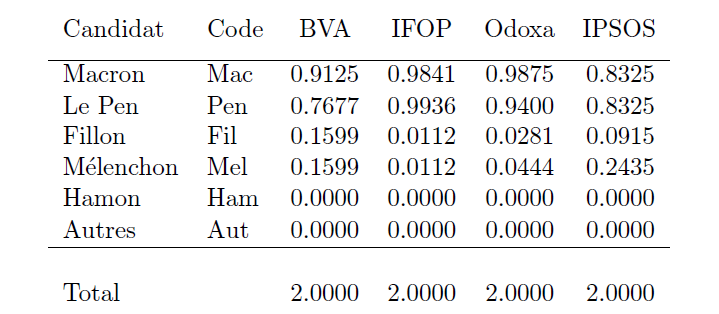
Plusieurs commentaires s’imposent :
- Rappelons d’abord qu’il n’y a pas de « vraie » probabilité et que chaque probabilité donnée ci-avant n’est que la traduction d’un certain état de connaissance. A chaque fois, il s’agit des connaissances provenant d’un seul sondage, en ne tenant aucun compte d’éventuelles informations extérieures à ce sondage.
- On notera ensuite que les probabilités s’additionnent à 2. Ceci est logique et n’est que la traduction probabiliste que deux candidats doivent nécessairement arriver dans les deux premiers.
- Les probabilités les plus élevées sont le résultat de la conjonction de : (i) une fréquence élevée, et/ou (ii) obtenue sur un effectif n grand. Ainsi les probabilités les plus fortes concernent Macron et Le Pen, dans les sondages IFOP (surtout parce que n est grand) et Odoxa (surtout parce que les écarts entre les Freel sont les plus nets).
- Quel que soit le sondage, les probabilités que Hamon ou un des « petits » candidats soient au second tour sont quasi nulles (à 0.0001 près).
- Au vu de ces sondages, tout se joue donc entre Macron, Le Pen, Fillon et Mélenchon. Les probabilités pour que Macron soit présent au second tour varient de 0.8325 à 0.9875 et celles de Le Pen varient de 0.7677 à 0.9936, selon les sondages. Ainsi, si d’après certains sondages on a une garantie élevée que ces deux candidats soient ceux du second tour, d’autres sondages ne permettent pas une conclusion aussi nette. En contrepartie, Fillon garde jusqu’à 0.1599 de probabilité d’être au second tour (BVA) et Mélenchon jusqu’à 0.2435 (IPSOS), soit presque une chance sur quatre. Ces résultats viennent donc confirmer ce que les marges d’erreur laissaient pressentir : l’incertitude, mesurée par les probabilités, reste encore grande.
• Enfin, toutes ces conclusions valent pour les Freel, qui sont des fréquences d’intention de vote telles qu’exprimées jusqu’au 14 avril. Et celles-ci ne sont que le reflet incertain des fréquences de vote effectif du 23 avril. La campagne n’est pas finie.
Télécharger l’article au format PDF dans sa version optimisée.
Références
Bernard J.-M. (2017a), « Aller au-delà des marges d’erreur dans les sondages d’intentions de vote »,
Bernard J.-M. (2017b), Logiciel BayCat Version 5.0.
Wikipedia (2017) : https://fr.wikipedia.org/wiki/ , Phrase-clé : « Liste de sondages sur l’élection présidentielle française de 2017 ».

